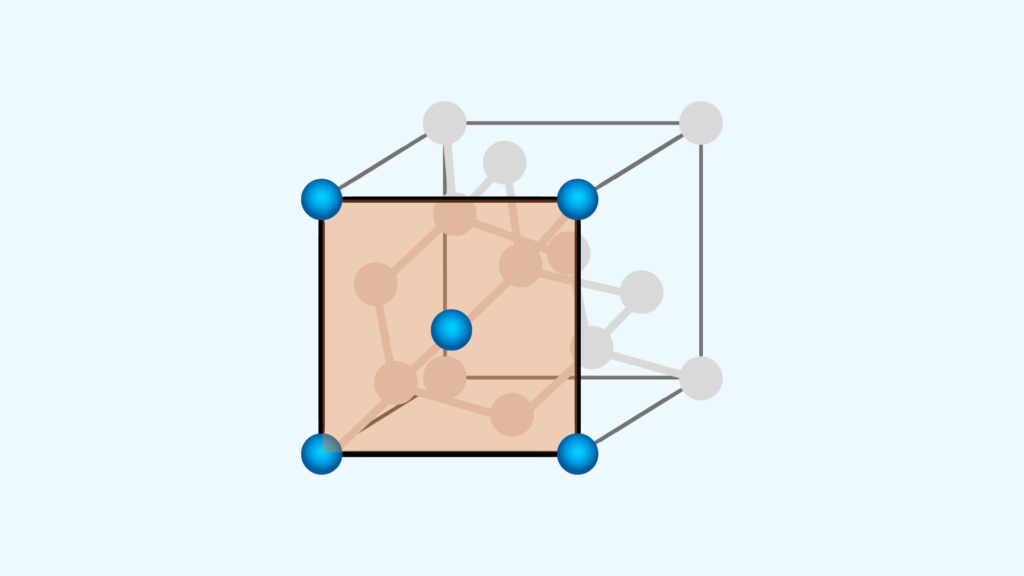
シリコンの結晶面と結晶方位:ミラー指数と面のなす角
面・方位のなす角計算ツール
ミラー指数を入力すると面・方位同士のなす角を計算できます(※立方晶のみ)。
面1:(h1k1l1)
面2:(h2k2l2)
なす角(°)
0°
シリコンの結晶面
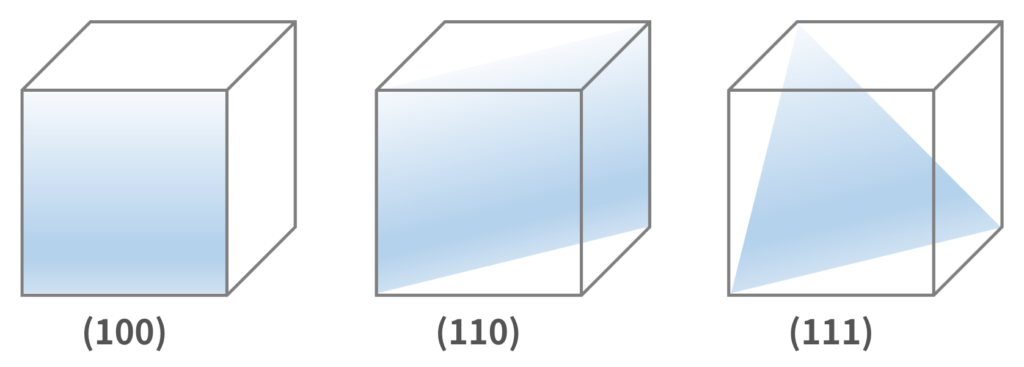
シリコン結晶の重要な結晶面は{100}・{110}・{111}の3面です。
半導体シリコンは単結晶です。すなわち、結晶の化学的・機械的・電気特性は結晶方位に大きく依存することが知られています。
例えば、p型MOSFETのキャリア移動度は(110)>(100)であることが知られています。また、面方位によってエッチング速度が大きく異なるため、エッチング速度差を利用することで様々な形状を形成することが出来ます。
このように、単結晶の面方位を理解することは非常に重要と言えます。
結晶面・方位の表し方:ミラー指数
単結晶は原子が規則正しく並んだ物質です。その中には、互いに平行かつ等間隔の距離で並んでいる原子の面が存在し、これを結晶面と呼びます。
結晶中には様々な結晶面が存在します。
特定の結晶面や結晶方位を記述するために用いられるのが「ミラー指数」です。
方向・結晶面のそれぞれの表し方について説明していきます。
方向の表し方
結晶方位は、座標の原点(0,0,0)を通り、その結晶面と垂直な方向です。
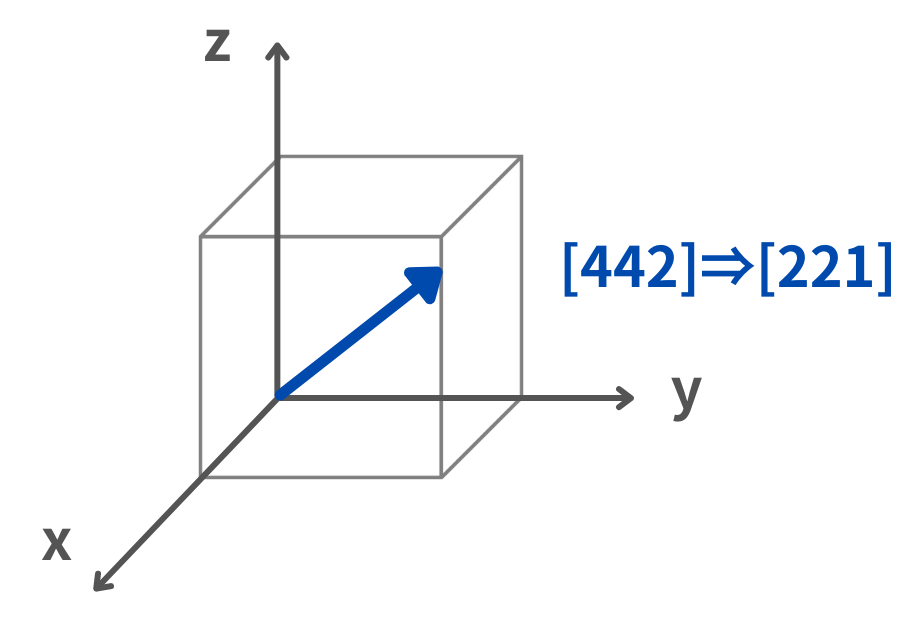
原点から点(H,K,L)へ向かう方向は、H:K:Lの最小の整数比h:k:lを用いて[hkl]と表します。座標が負の場合には、数字の上にバーを書きます。
すなわち、[221]方向は(221)面に垂直な方向(法線方向)です。
方向の表し方の例を見てみましょう。
- 例1) 座標(1,1,5)に向かう方向=[115]
- 例2) 座標(2,2,4)に向かう方向=[112]
- 例3) 座標(-2,1,5)に向かう方向=[215]
鍵カッコ[]は特定の方向を表します。立方晶系では[hkl]や[lhk]、[hlk]は全て等価であり、山カッコ<>を用いてまとめて
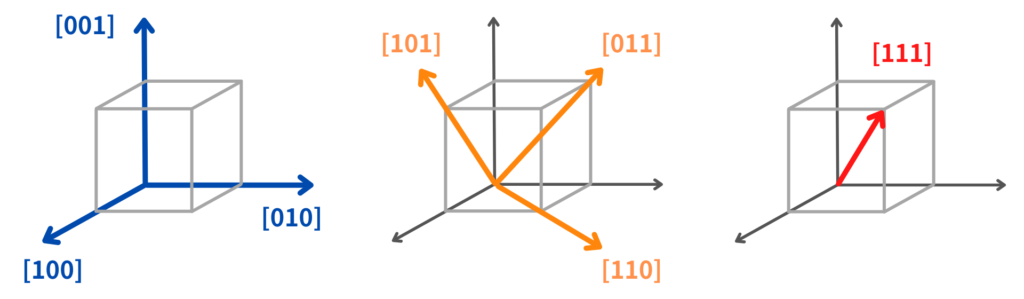
下記に代表的な方向の例を図示しました。
例えば、立方晶系において[100]・[010]・[001]は等価であり、まとめて<100>と表します。
面の表し方
ミラー指数による結晶面の算出は以下の通りです。
- 結晶面と各軸との交点座標(x,y,z)を求める
- 座標(x,y,z)を各格子定数で割り、その逆数を求める
- h,k,lを最小整数比に直し括弧()で囲む
$$h=\frac{a}{x}, k=\frac{b}{y}, l=\frac{c}{z}$$
$$(hkl)=(336)⇒(112)$$
ミラー指数の算出例は以下の通りです。
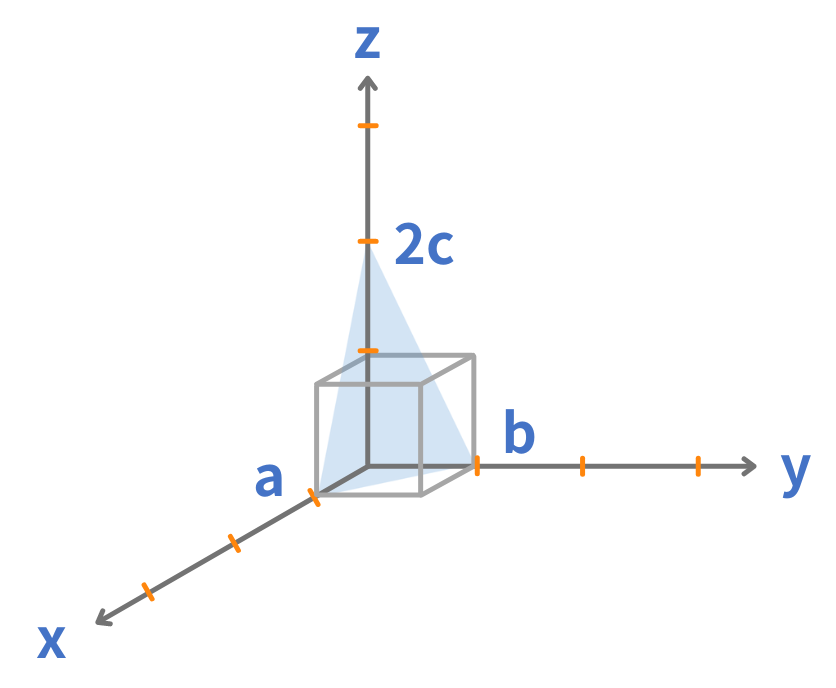
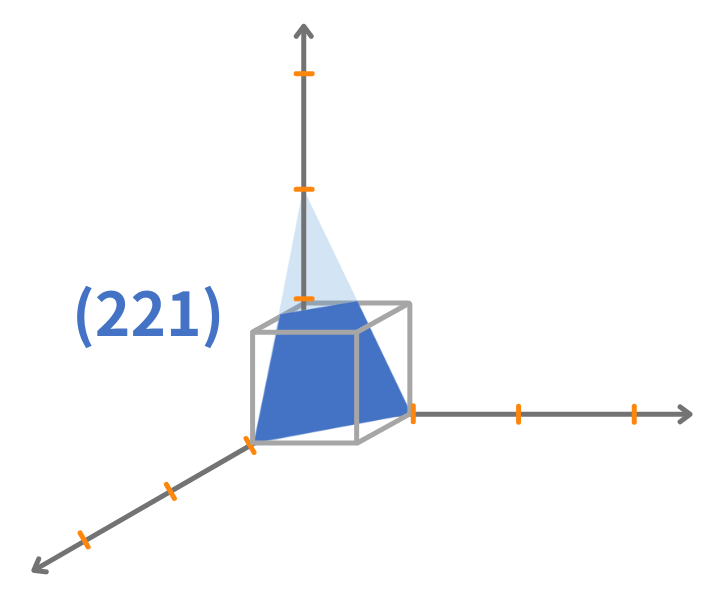
例として、x軸とa、y軸とb、z軸と2cで交点を持つ面:(x,y,z)=(a,b,2c)を考えます。
格子定数をメモリとする座標軸x,y,zを考えます。結晶面の座標(a,b,2c)を各軸の格子定数a,b,cで割り、逆数を取ります。
$$h=\frac{a}{a}、k=\frac{b}{b}、 l=\frac{c}{2c}$$ $$すなわち、h=1、k=1、l=\frac{1}{2}$$
算出したh,k,lに対し最小の整数比を求めます。
$$h:k:l=1:1:\frac{1}{2}=2:2:1$$
すなわち、この結晶面のミラー指数は(221)となります。
なお、ある面が座標軸と交わらない場合には、その軸のミラー指数は0となります。
例えば、x軸とa、y軸とb、z軸と平行(交わらない)結晶面は
$$h:k:l=1:1:\frac{1}{∞}=1:1:0$$
すなわち(110)面となります。
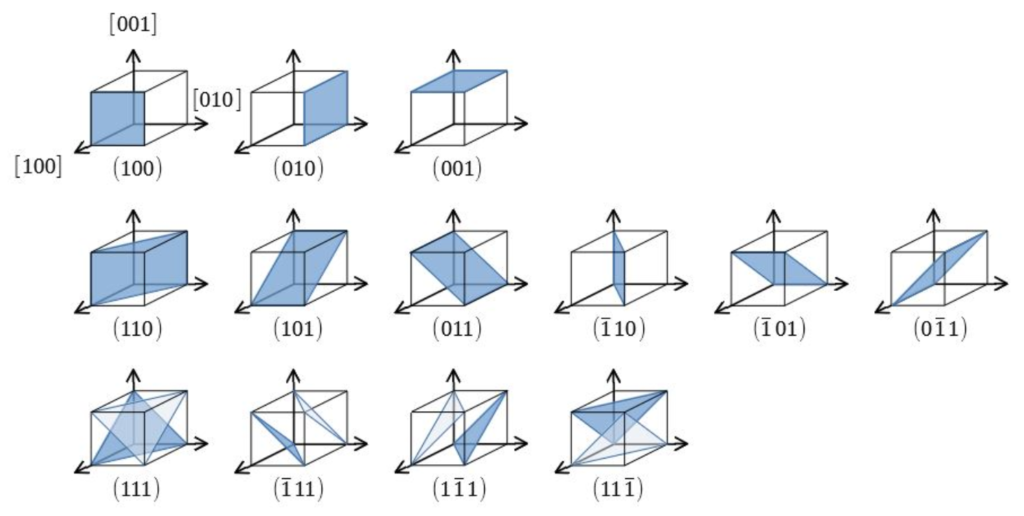
シリコンで重要となる{100}・{110}・{111}面の一覧は以下の通りです。
等価な方向・面の表し方
結晶格子の対称性によって、異なるミラー指数を有する結晶面や方向でも等価である場合があります。
結晶学的に等価な面や方位は以下の様に表記します。
{100}=(100), (010), (001), (100), (010), (001)
<100>=[100], [010], [001], [100], [010], [001]
例えば、下図はシリコンの(100)・(010)・(001)面です。
どの面も原子の並びが同一であり、結晶学的に等価であることが分かります。これらの面はまとめて{100}と表記します。
面のなす角の公式
内積の公式から、立方晶系における面同士のなす角は下式で求めることが出来ます。
$$\cos\theta=\frac{h_{1}h_{2}+k_{1}k_{2}+l_{1}l_{2}}{\sqrt{{h_{1}}^{2}+{k_{1}}^{2}+{l_{1}}^{2}} \times \sqrt{{h_{2}}^{2}+{k_{2}}^{2}+{l_{2}}^{2}}}$$
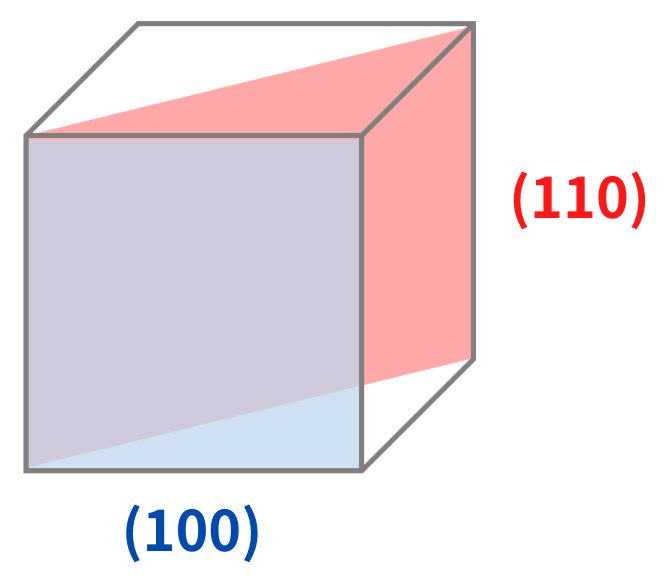
例えば、シリコンの(100)面と(110)面のなす角を求めてみましょう。
$$\cos\theta=\frac{1 \times 1+0 \times 1+0 \times 0}{\sqrt{{1}^{2}+{0}^{2}+{0}^{2}} \times \sqrt{{1}^{2}+{1}^{2}+{0}^{2}}}$$
$$\cos\theta=\frac {1}{\sqrt{2}}、\theta=45°$$
(100)面と(110)面のなす角は45°となります。
前の講座
次の講座