ホール効果測定とは:キャリア移動度の測定原理
ホール効果測定とは?
ホール効果測定は「磁場中の半導体試料に電流を流した際に発生する電場(ホール電場)を測定する手法」です。
電子・正孔のキャリア移動度を算出することが可能です。
ホール効果測定は半導体のキャリア移動度を算出するのに最もよく用いられる手法です。
ホール効果測定により求めたキャリア移動度はホール移動度(Hall)とも呼ばれます。<なお、ホール効果(Hall)のHallは人名であり、正孔のholeとは異なります。
ホール効果とは
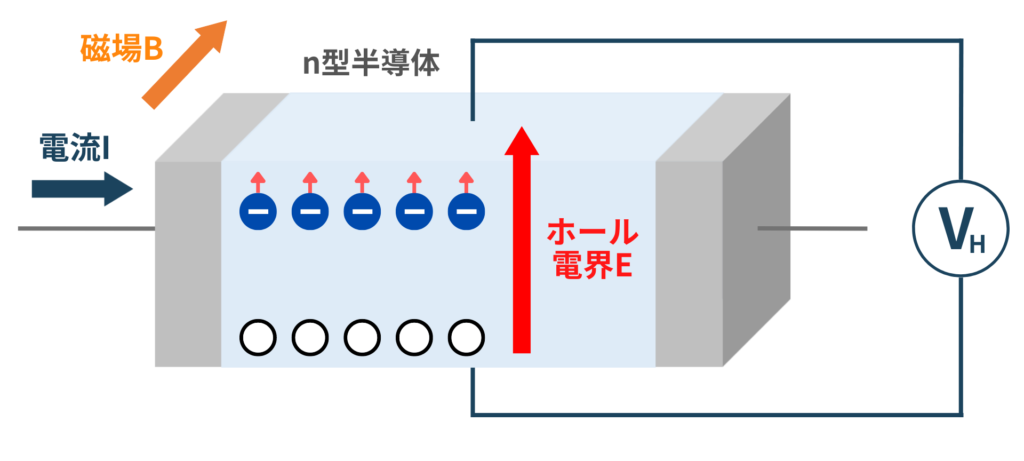
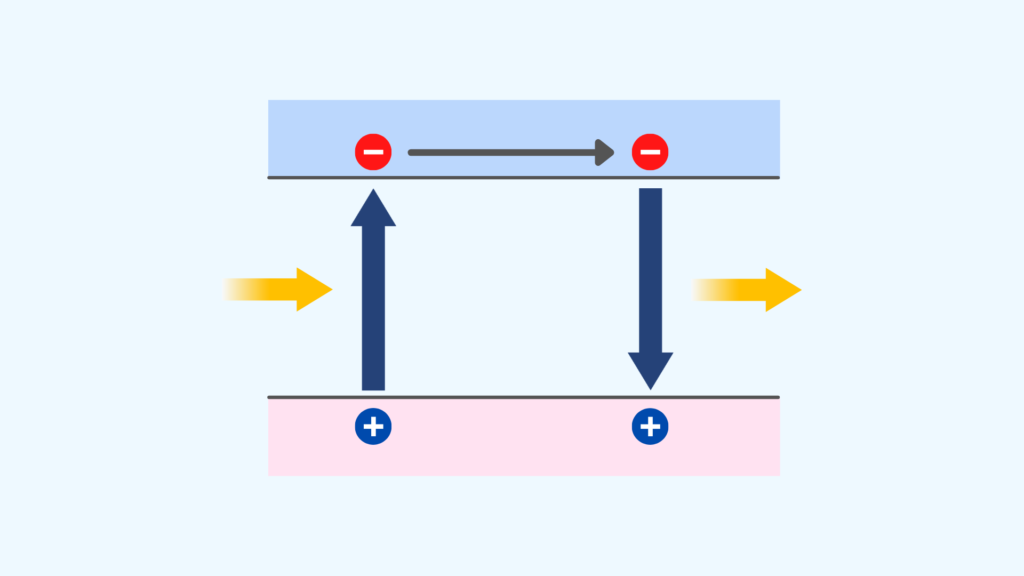
下図はn型半導体のホール効果の模式図です。
ホール効果とは「半導体試料に一定方向の電流を流し、電流に対し直交する方向に磁場を印加すると、電流と磁場の両方に直交する方向に電場(ホール電場)が発生する現象」です。
磁場中のn型半導体に電流を流すと、荷電粒子はローレンツ力を受けます。上図の場合、n型半導体の多数キャリアである電子は上面に集まり、負に帯電します。反対に、下面側は正に帯電します(半導体中のキャリアの偏りが変わっている)。
この電荷の偏りのによる電界(起電力)をホール電場と呼びます。ホール電場による起電力の発生をホール効果と呼びます。ホール効果による起電力を電圧計で測定するのがホール効果測定です。上図の例では、下面から上面に向かうホール電界が発生します。
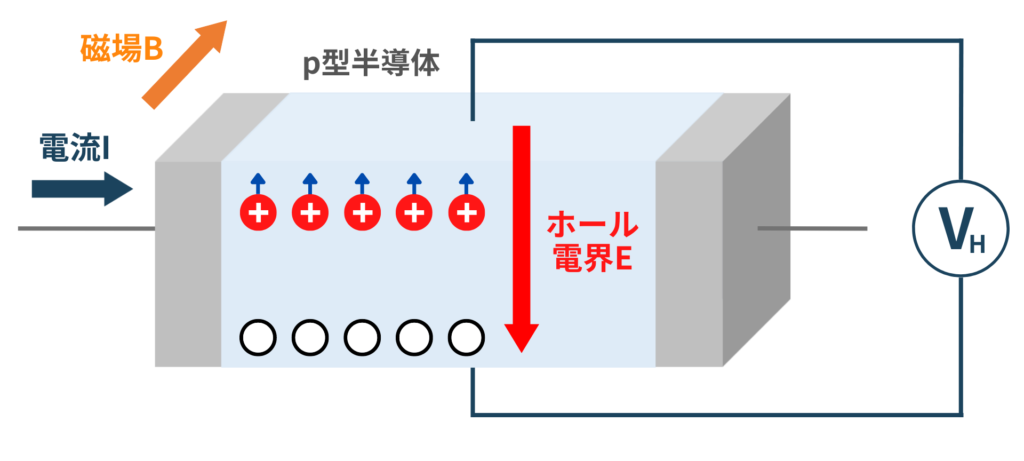
p型半導体のホール効果もn型と同様に考えることが出来ます。(下図)。
p型半導体の場合には、多数キャリアである正孔は同じようにローレンツ力を受け、上面に集まり正に帯電します。反対に下面は負に帯電します。結果として、上面から下面へ向かうホール電界が生じます。
n型半導体・p型半導体により発生するホール電圧VHの符号が変わるため、ホール効果測定を行うことで、半導体の判定を行うことが出来ます。
ホール効果測定で分かること
ホール効果測定では、抵抗率(ρ)とホール電圧VHのデータを得ることが出来ます。得られたデータを解析することで、
- 半導体のpn判定
- 多数キャリア濃度
- 多数キャリア移動度
の物性値を算出することができます。
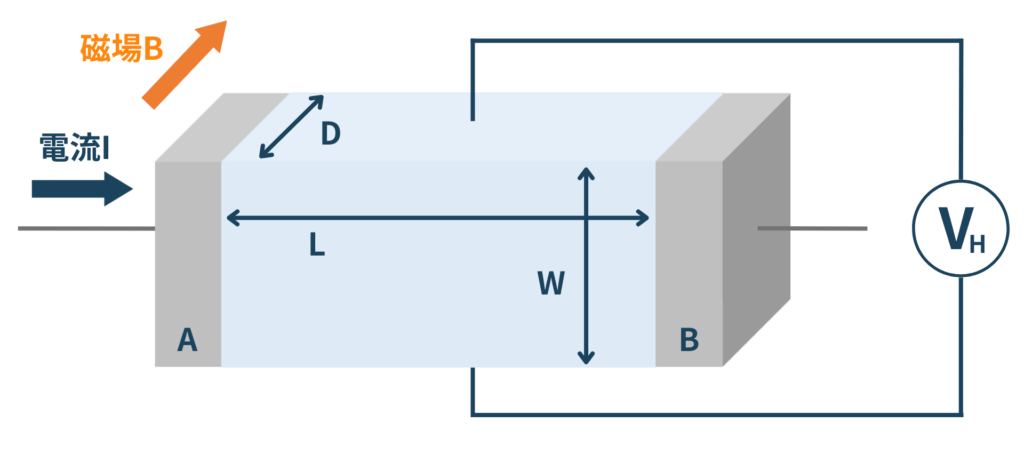
電極AB間に電圧Vを印加した際に流れる電流Iから、抵抗率(ρ)を算出することが出来ます(オームの法則)。また、電圧計を用い、ホール効果によるホール電圧VHを測定することが出来ます。
ホール電圧VHの符号から、PN判定を行うことが出来ます。
また、キャリア濃度(n)は以下の(1)式・(2)式から算出することが出来ます。
$$\tag{1}V_H = {R_H} \cdot {\frac{IB}{D}} $$
$$\tag{2}R_H = {\frac{1}{qn}} $$
VH:ホール電圧、 RH:ホール係数、 I:電流、 B:磁束密度、 q:電荷素量、 n:多数キャリア濃度
(2)式より、RHが負の場合にはn型半導体、正の場合にはp型半導体であることが分かります。
更に、下式より多数キャリア移動度を算出することが出来ます。
$$\tag{3}μ = \frac{1}{qnρ} $$
μ:多数キャリア移動度、 q:電荷素量、 n:多数キャリア濃度、 ρ:抵抗率
測定方法:van der Paul法
ホール効果測定は、主にvan der Paul法と呼ばれる手法で行われます。
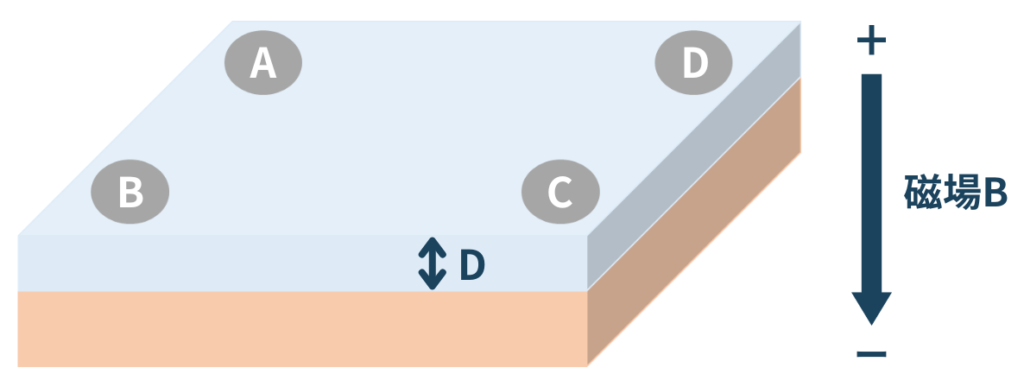
van der Paul法では、四角形状のサンプルを用います。
抵抗率ρおよび多数キャリア移動度μの測定は以下の手順で行います。
- 電極AB間に電流IABを流し、電極DC間の電圧VDCを測定
- 下式より抵抗値RAB,DCを求める
- 同様の手順でRBC,ADを求める
- 以下式から抵抗率ρを求める
- 電極Aから電極Cに電流IACを流し、上方から下方に磁場を印加した際に、電極DB間に発生する電圧VDBを測定
- 理想的にはVDB=VH IAC=Iのため、式(1)・式(2)から多数キャリア密度nを算出される
- 下式から多数キャリアの移動度μを求める
$$\tag{4}R_{AB,DC} = \frac{V_{DC}}{I_{AB}} $$
$$\tag{5}ρ = \frac{\pi D}{\ln2} \cdot \frac{(R_{AB,DC}+R_{BC,AD})}{2} \cdot f $$
$$\tag{6} \left| \frac{(R_{AB,DC}+R_{BC,AD})-(R_{AB,DC}+R_{BC,AD})}{(R_{AB,DC}+R_{BC,AD})+(R_{AB,DC}+R_{BC,AD})}\right| = \frac{f}{\ln2}arccosh \left[\frac{exp\frac{ln2}{2}}{f}\right]$$
$$\tag{7}μ = \frac{1}{qnρ} $$