ラマン分光法(Raman)とは:測定原理と応用例
ラマン分光法とは?
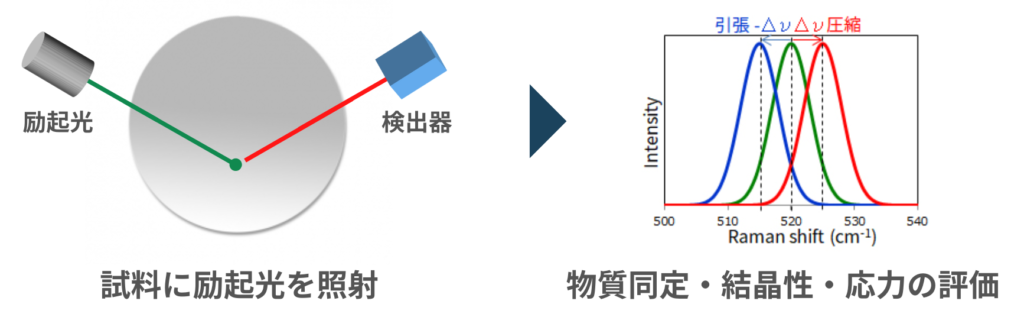
ラマン分光法(Raman)は「物質に光を照射した際に発生する"ラマン光"を用いて、物質を評価する手法」です。
ラマン分光法により得られたラマンスペクトルを分析することにより、
- 化学結合・物質の同定
- 結晶性
- 応力・歪み
などの物性を評価することが出来ます。
ラマン散乱光とは
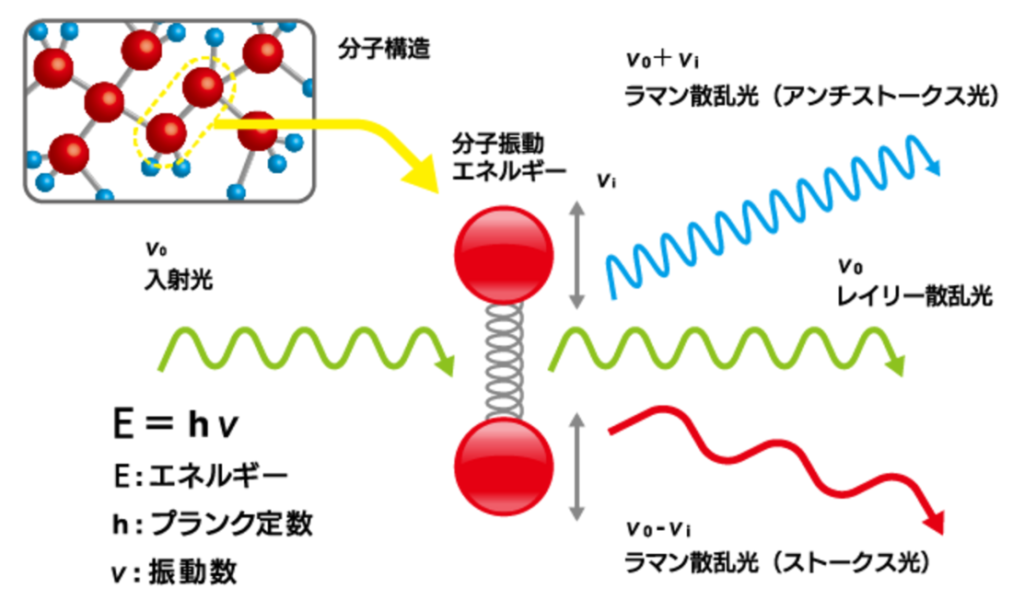
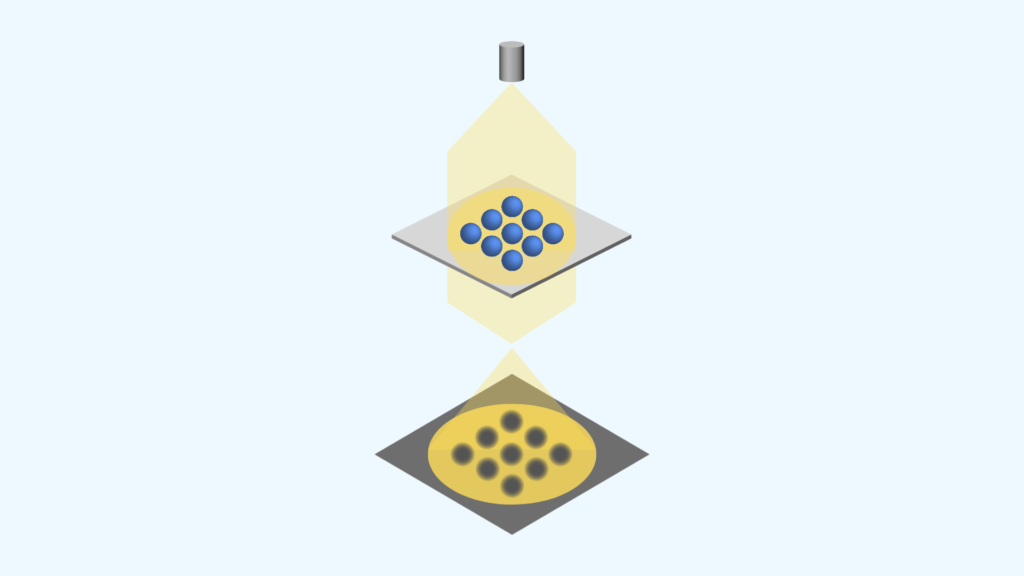
物質に光を照射すると、物質を構成する分子と衝突し、光の一部は散乱されます。
散乱光の波長の内、99.99%以上は入射光と同じ波長(レイリー散乱光)ですが、0.01%以下の極僅かな成分として、入射光と異なる波長の光が含まれています。これをラマン散乱光と呼びます。
ラマン光は、散乱光の大部分を占めるレイリー散乱光の強度に対し10-6(100万分の1)の強度の極めて微弱な光です。そのため、実際の測定には高強度なレーザー光を照射する必要があります。
入射光とラマン散乱光のエネルギー差は、分子・結晶構造を反映しているため、ラマン分光法で物質同定や結晶性評価が可能となります。
ラマン光が発生する原理をもう少し詳しく見て行きましょう。
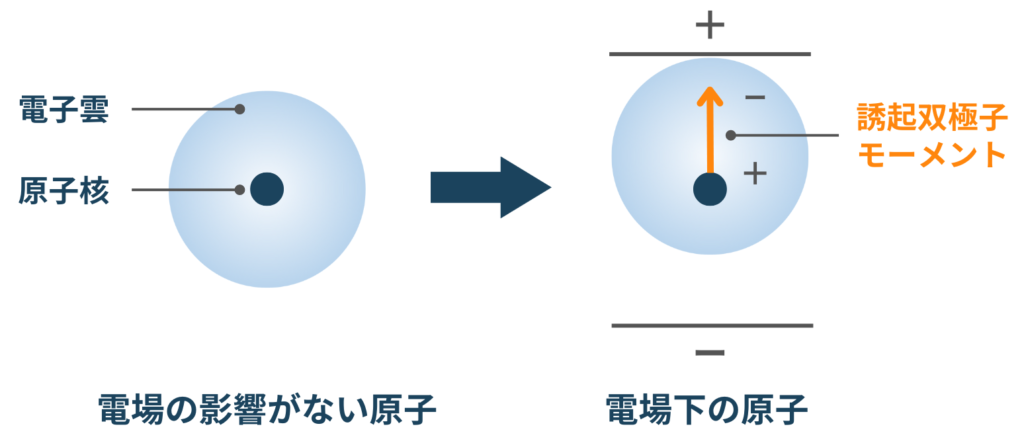
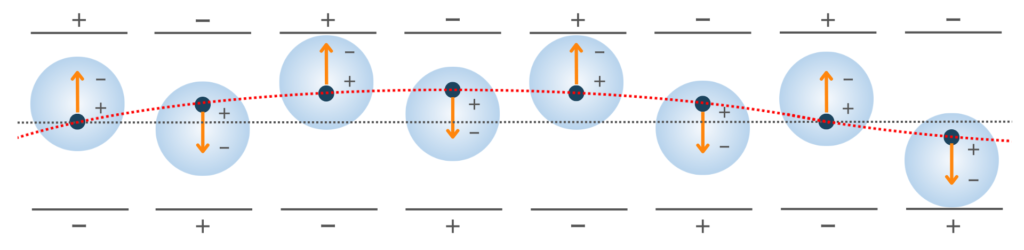
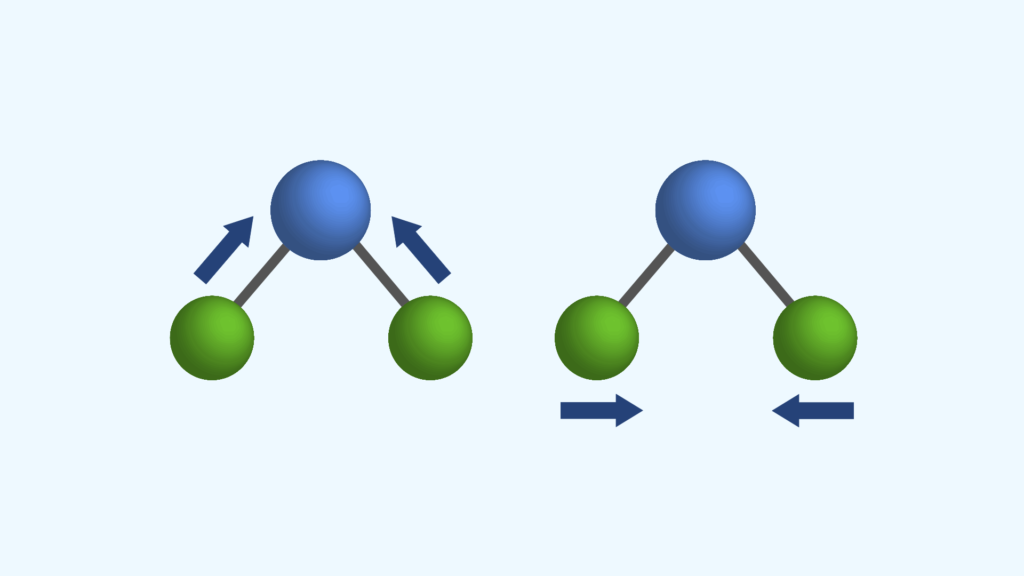
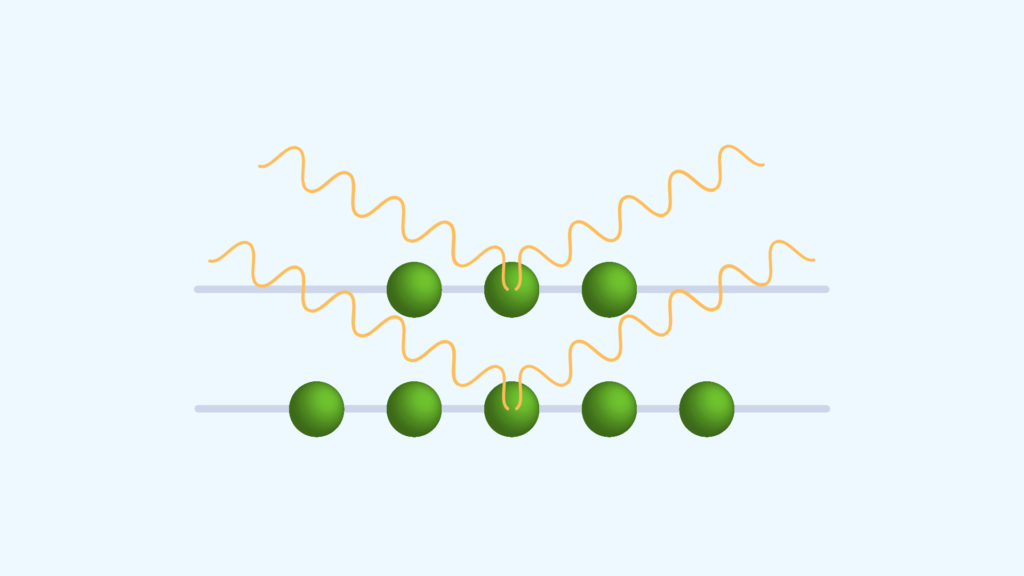
ラマン光を理解するためには双極子モーメントの理解が必要です。光は電磁波の1種であり、周期的に電場を形成しています。
分子に光が照射されると、光の電場により電子雲が歪み、原子核と電子雲の重心にズレが生じます。原子核の正と電子雲の負の重心のズレ、すなわち、分極の度合いを「双極子(diple)」、正から負に向かうベクトルを「双極子モーメント(dipole moment)」と呼びます。
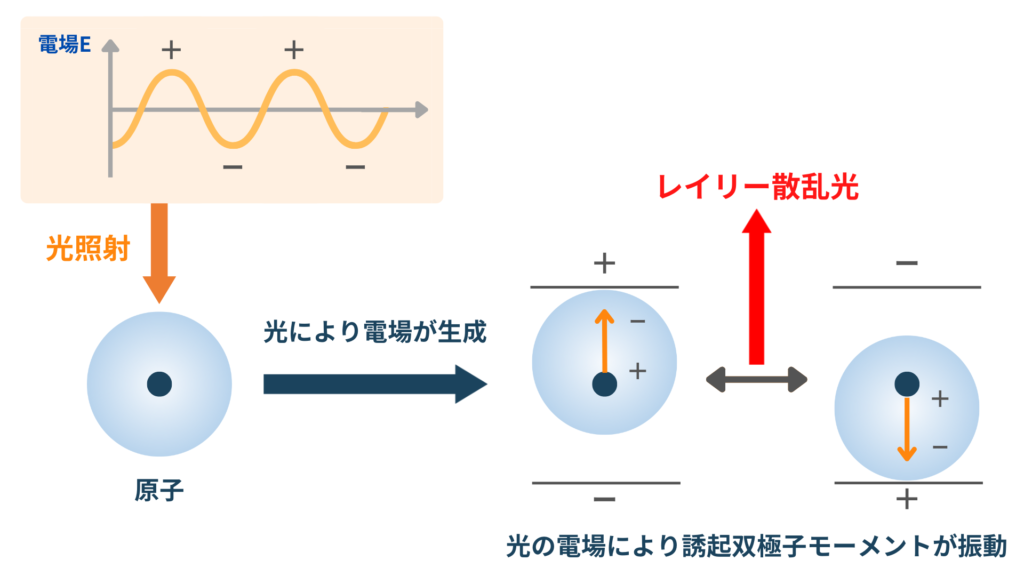
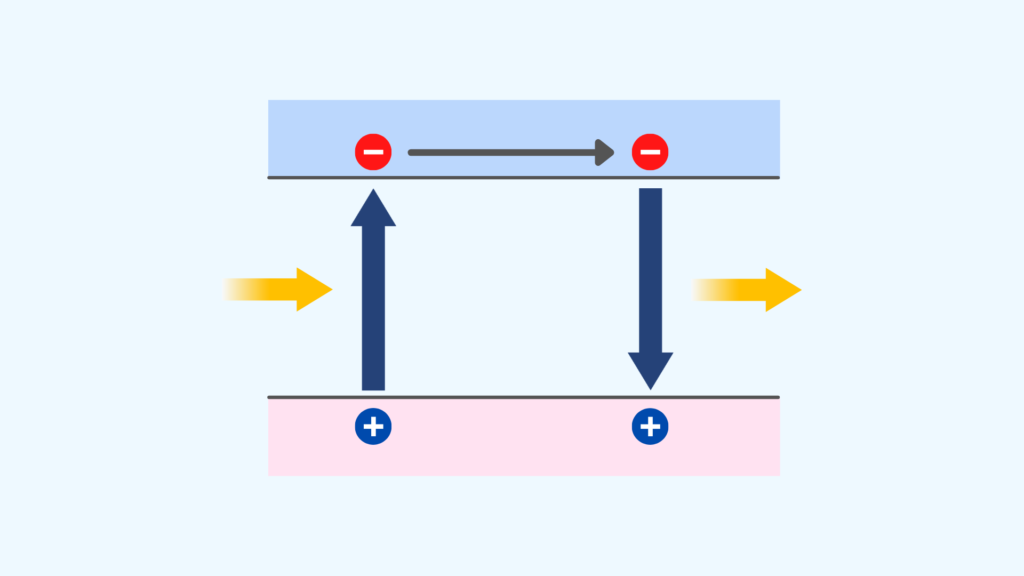
双極子モーメントの観点からレイリー散乱光を理解しましょう。
光は電磁波であり、周期的に正負の電場を形成しています。原子に光が照射されると、電場に誘起された双極子モーメントも振動し、入射光と同じ波長の散乱光が放出されます。これがレイリー散乱光が発生する原理です。
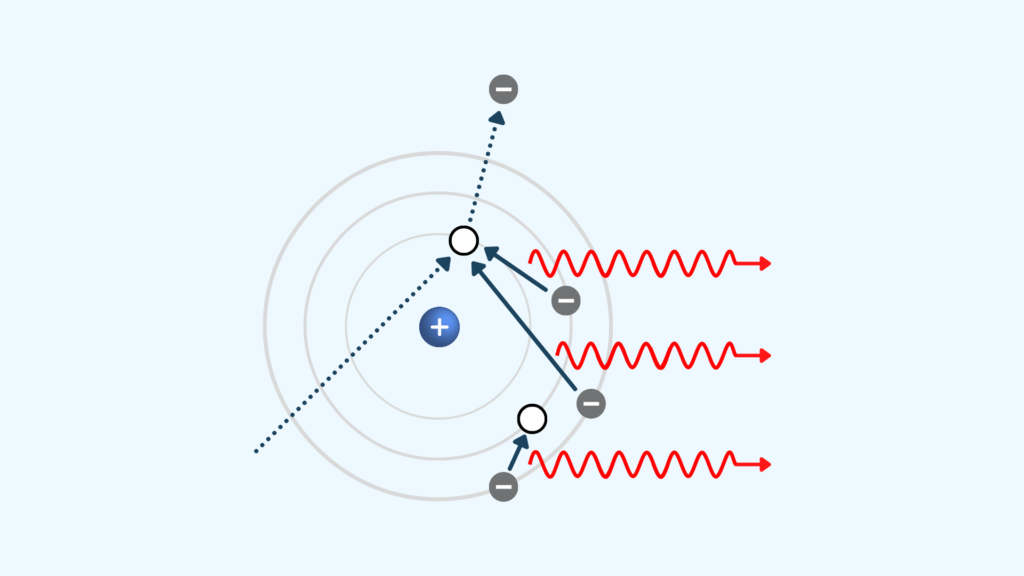
では、ラマン散乱光の発生原理はどうでしょうか。
先ほどは電子のみの振動を考えましたが、実際の原子では原子核も振動しています(電子よりも2000倍重い為、振動数は小さい)。
光の電場の振動(電子雲の振動)と原子核の振動が干渉し、入射光波長とは異なる双極子モーメントの振動が生じます。これがラマン散乱光です。
ラマンスペクトル
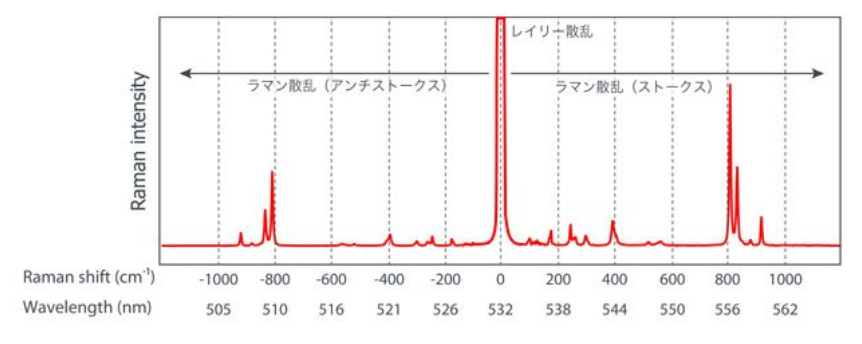
下図はラマンスペクトルの例です。
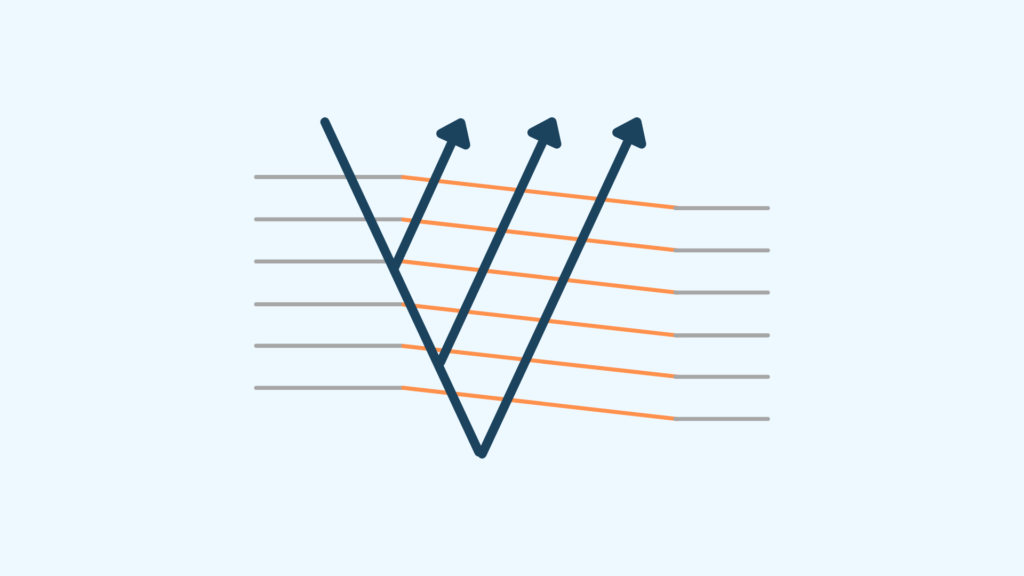
ラマンスペクトルでは、入射光と同じ波長のレイリー散乱光に対し、レイリー散乱光より長波長側および短波長の両方にラマン散乱光が検出されます。
長波長側のラマン散乱をストークス線、低波長側をアンチストークス線と呼びます。
ラマン分光法ではより強度の強いストークス線を用いて解析を行います。ラマン散乱光は実際に目で見て確認することが出来ます。下記の動画が非常にわかりやすくおすすめです。
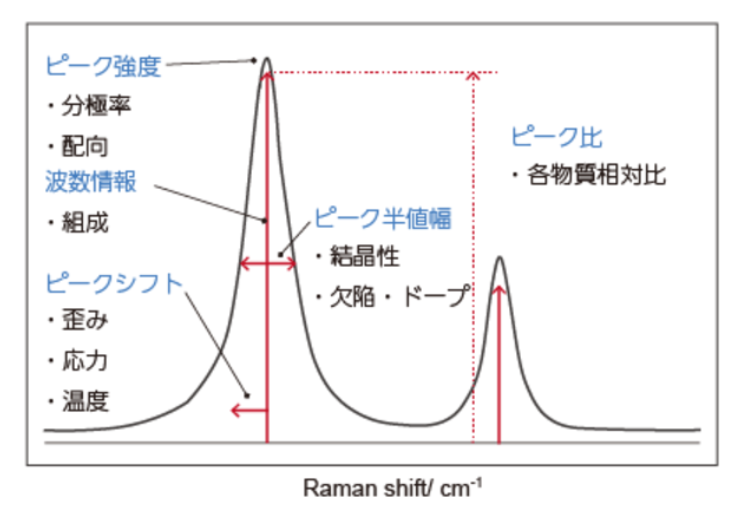
ラマンスペクトルのピーク位置や、ピークシフト量(ラマンシフト)の解析から、以下の様な幅広い物性評価が可能です。
ラマン散乱光は物質の結晶構造や分子振動に起因するため、応力による歪みや結晶性によっては波長が変化します。そのため、スペクトルを解析することが物性評価が可能なのです。
応用例
Si基板の応力分布
結晶に応力が加わると原子間距離が変わるため、原子の結合力も変化します。それに応じて格子振動の周波数も変化することから、応力によりラマン散乱光の波長もシフトします。
ラマン散乱光のシフトは圧縮応力で高波数側、引張応力で低波数側にシフトすることから、ラマンで応力評価が可能です。上図はSi基板に対して4点曲げで応力を加え、ラマンシフトを測定した例です。
ラマンシフト量から応力分布を可視化した結果、基板下側に圧縮応力、基板上側に引っ張り応力が確認されています。
半導体の微小応力測定
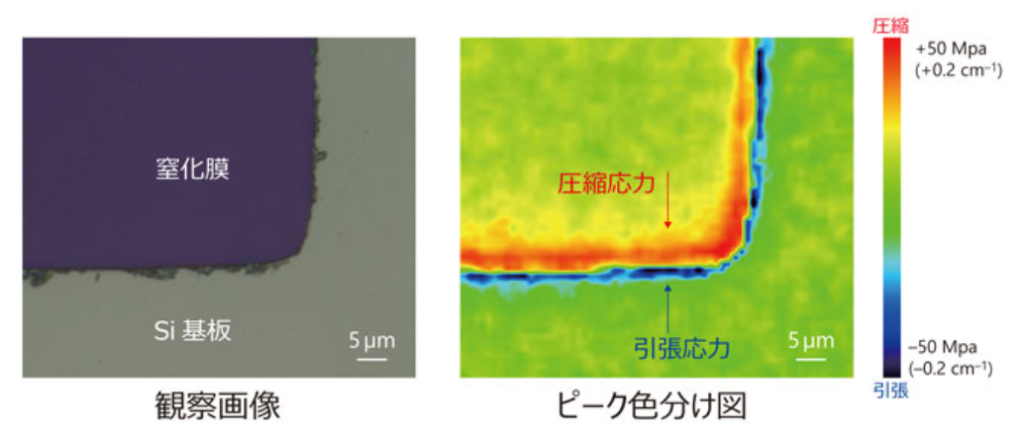
半導体デバイス作成時には、異種材料の成膜により基板に応力が掛かります。デバイスの微小な応力もラマンで測定可能です。
シリコン窒化膜(SiN)はエッチングの保護層として用いらます。Si基板と窒化膜の境界に圧縮応力および引張応力が印加されていることが分かりました。
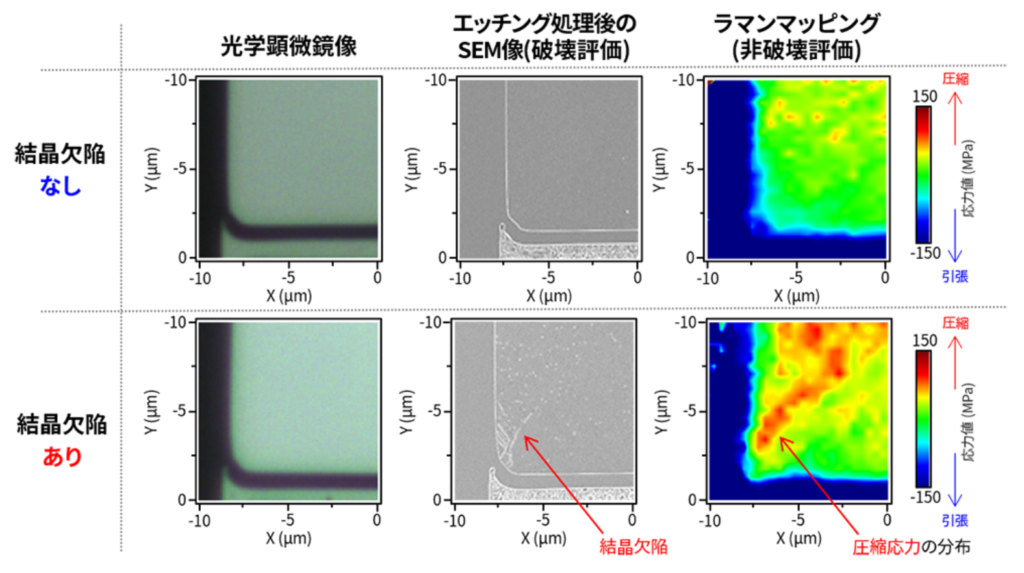
デバイス中Si層の結晶欠陥評価
酸素析出部や転位などの結晶欠陥の周辺には局所的な応力やひずみが生じています。この応力分布についてもラマンで評価可能です。
SEMで確認される結晶欠陥周辺のラマンマッピングを確認した結果、欠陥近辺だけでなく幅広い領域にわたる100MPaの圧縮応力が加わっていることが分かりました。
このように、ラマンは光学顕微鏡やSEM(電子顕微鏡)などで観察できない微小な応力を非破壊で可視化することが出来ます。